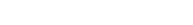Pip Wangler implementation

The underlying implementation of Mousepickle’s Pip Wangler application might be of interest to other developers, so some insight is given here on two specific aspects of the coding - the modelling of the bendy Wangle Wire itself, and some of the optimisations made to the OpenGL vertex and fragment shaders.

A separate page is provided in case you’d prefer just to learn how to use Pip Wangler.

---

Modelling the wire

First a gentle warning: You’ll probably need to have some grounding in the relevant maths to grasp this in full - especially in the absence of any supporting illustrations!

In one sense the wire is modelled a completely straight: A series of segments are described very simply to form a ‘map’ of the wire, with the xyz coordinates of the starting point and an initial direction being followed be lengths of wire that start in one direction, and end in another. If the start and end directions are the same it’s a straight section; otherwise it’s an ‘elbow’ piece.

We can then traverse the map and precalculate the xyz coordinates of the start and end of each segment, and also the total elapsed length along the wire at the start and end of the segment. Then at runtime we slide the Pip along this linear model and can determine at once which segment we’re in, and how far along it we are.

It’s relatively simply to work out the direction of the wire at the point where the Pip currently resides, and that gives us the starting point for the physics modelling. We can determine the component of ‘gravity’ (down the screen) that’s in line with the wire, for example, and can accelerate the Pip - along the linear model - accordingly. Add a bit of wind resistance and ‘grind’ and away you go!

This effectively perfect model of the wire is the one used when calculating the score and so on.

In parallel with that perfect mathematical model of the Wire we also create a (good) approximation of the wire as a largeish set of vertices (grouped into triangular facets) that we can hand down to OpenGL for rendering.

The magic applied here is three-fold. Firstly the vertex positions are calculated by sweeping a ring of pre-calculated vertices along the wire path. Some helper functions translate and rotate the ring, and when we go around an elbow we stop off at more or fewer waypoints around the corner depending on the radius of the bend. The number of waypoints around an elbow is based on the square root of the radius, so that we concentrate our expenditure on elbow-smoothing vertices and facets (and they are expensive in terms of rendering) on the sharper corners.

Secondly, the ring of pre-calculated vertices contains twice as many points as you might think necessary for a given smoothness. Think of them as sets A and B, interleaved. At each waypoint we switch between the two sets, so we’re stitching the A points from one ring with the B points from the next. Then those B points to the A points from the ring after that.

This is where a diagram might really help, but try imagining the way a toy snare drum has cord threaded up and down around the cylindrical surface.

Interleaving in this way means that we only need to rotate the ring around the axes that lie in the ring’s plane, never the axis perpendicular to it.

Thirdly, the normal vector for every vertex is the normalised vector from the middle of our swept ring to the vertex, so no additional calculation is required for that.

Note that the xyz coordinates of the Pip at any moment are calculated from the perfect model, so even when the Wire appears to be a bit approximate - where there are a finite number of straight lengths making up a corner, for example - the Pip itself moves on screen completely smoothly.

OpenGL ES 2

Pip Wangler uses OpenGL ES 2, which gives much slicker rendering than we saw in, for example, Tinkerball, which used OpenGL ES 1.1.

Exemplar OpenGL shader code seems to be pretty thin on the ground, on the Internet at least (there are books covering the subject), but that shouldn’t deter developers! One approach is to start with a vanilla, unoptimised, pair of vertex and fragment shaders, and to get those rendering nicely, and then add (again, unoptimised) a very bland diffuse and specular lighting algorithm.

Optimisation is key to getting decent performance, particularly on a complex model, but in some ways that’s the easy part. The documentation - including application development and optimisation tips - available around the PowerVR SGX chipset is superb, the Khronos Group have produced a colourful cheat sheet that gives a lovely overview, and Apple also provide their developers with clear guidelines.

Taken together these sources advise you to do thing like...

• Calculating per vertex, rather than per fragment
• Leveraging the interpolation of vertex shader outputs
• Pre-calculating / pre-baking where possible
• Using iOS developer tools for OpenGL profiling on your test devices

... none of which are very surprising, perhaps. There are many more tips than those, and a couple of hours spent optimising was enough to double or treble the achievable frame rate for Pip Wangler. Performing the optimisation with the detail on the Wire model turned up very high allowed us to observe the effect of changes to shader code fairly precisely.

Now... starting with an unoptimised pair of shaders allows you to keep the underlying maths firmly in mind; that maths is all very well described in Wikipedia and elsewhere. With the maths in mind you can introduce some nice optimisations as you shift calculations up from fragment to vertex shader, maybe with some swizzling, and from vertex shader out into the iOS code. Understanding how the calculations give rise to the final rendered image gives you scope to reduce render times through sensible approximations, which can give you greater performance increases than mere refactorings.

Pip Wangler does make use of one particularly natty optimisation, which seemed novel at the time: We approximate higher-power specular shading with a smoothstep function, that’s less expensive than a pow. That mightn’t be appropriate for every kind of model, of course; the Wangle Wire has quite a tightly curved surface at every point, because the radius of the wire itself is relatively small, and that clearly makes Pip Wangler something of a special case.

Lastly: To change the style of rendering of the Wangle Wire we simply switch active shaders at runtime; something with almost no run-time effort involved. There’s a little magic to be done around accessing the uniforms and attributes for multiple shader programs efficiently, but that’s more a question of iOS development than one of OpenGL as such.

---

Wangle Wire vertex shader, from Pip Wangler

This is provided with only minimal commentary, and would only make complete sense with the corresponding fragment shaders, but it does show where some of the optimisation was carried out.

precision mediump float;
// 1. Always consider, and specify precisions. We explicitly default to mediump here.

attribute highp vec4 SourcePosition;
attribute highp vec3 SourceNormal;

uniform mat4 Projection;
uniform vec4 Model[3];

// 2. Lights for the Pip itself, and red, green ends of the Wire.
uniform vec3 LightPosition0;
uniform vec3 LightPosition1;
uniform vec3 LightPosition2;

// 3. Varying output from the vertex shader. Will be interpolated.
varying vec4 DestinationNormal;
varying vec4 DestinationPosition;
varying vec4 LightVector0;
varying vec4 LightVector1;
varying vec4 LightVector2;

uniform highp float BandOffset;
// 4. This is used in fragment shaders only.

void main(void) {
    vec4 pModel;
    
    // 5. Cheaper matrix maths possible?
    pModel.x = dot(Model[0], vec4(SourcePosition.xyz, 1.0));
    pModel.y = dot(Model[1], vec4(SourcePosition.xyz, 1.0));
    pModel.z = dot(Model[2], vec4(SourcePosition.xyz, 1.0));
    pModel.w = 1.0;

    gl_Position = Projection * pModel;
    
    DestinationPosition.xyz = normalize(pModel.xyz);
    // 6. Normalised vector from viewpoint to surface, ready for lighting algorithms.
    DestinationPosition.w = SourcePosition.w;
    // 7. Spare w component used to pass on (and interpolate) the elapsed distance along the Wire.

    // 8. More pre-baking for lighting algorithms. The raw normals are not required.
    DestinationNormal.x = dot(Model[0].xyz, SourceNormal);
    DestinationNormal.y = dot(Model[1].xyz, SourceNormal);
    DestinationNormal.z = dot(Model[2].xyz, SourceNormal);
    DestinationNormal.w = dot(DestinationNormal.xyz, DestinationPosition.xyz)
    	* 15000.0 / (pModel.z * pModel.z * pModel.z);
    
    // 9. Only relative position to lights need be passed to fragment shader.
    vec3 LV0 = LightPosition0 - pModel.xyz;
    vec3 LV1 = LightPosition1 - pModel.xyz;
    vec3 LV2 = LightPosition2 - pModel.xyz;
    
    LightVector0.xyz = LV0;
    LightVector1.xyz = LV1;
    LightVector2.xyz = LV2;
    
    float distance = length(LV0);
    // 10. Interpolate / approximate attenuation distance from light sources.
    LightVector0.w = distance * distance;
    // 11. Again, store efficiently in unused w.
    distance = length(LV1);
    LightVector1.w = distance * distance;
    distance = length(LV2);
    LightVector2.w = distance * distance;
}

A warning about point one (specifying precisions). It’s not always obvious which precision is actually the best to use in a given situation. The available documentation (especially the PowerVR documents) is very good on this; it’s well worth reading properly.

---

Apple’s review process

The transition from uploaded to ‘in review’ status took a shade over a week. The review itself was relatively brief, and as usual we assume that reflects the self-contained nature of the application.